External brilliance - luster

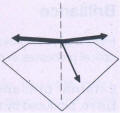
fig 182 Reflection of light on the surface of a stone A ray of light which falls on the surface of a diamond is split into two partial rays. Whilst one part of the ray enters the diamond, the remaining light component is reflected back from the surface of the stone, and this occurs at the same angle ,to the normal of the surface N as that at which it meets the surface (Fig 182).
By the luster of a gemstone - and in diamond it is very marked and is described as "adamantine" - is understood the totality of the light reflected at the surface.

Fig 183 The amount of light reflected is dependent on the angle of incidence Fig 183 The amount of light reflected is dependent on the angle of incidence Fig 183 The amount of light reflected is dependent on the angle of incidence
Fig 183 The amount of light reflected is dependent on the angle of incidence

The proportion of light reflected is dependent on the angle of incidence. As shown in the examples of different angles of incidence in Fig 183, it is the greater, the flatter the angle at which the light falls on the surface. When the light falls perpendicularly the greater part of it penetrates through the surface into the stone. With increasing angles of incidence, the luster intensity increases, and at E (the angle of incidence) = 70°, reaches about 27 % of the total incident light. Only when the light strikes the surface almost horizontally does the luster exceed the internal brilliance and dispersion.

Angle of incidence in air Proportion of light reflected Proportion of light refracted
10° 17,23 % 82.77 %
20° 17.?3 % . 82.77 %
30° 17.36% 82.64 %
40° 17,73 % 82.27 %
50° 18.73 % 81,27 %
60° 21.12 % 78,88 %
70° 27.21 % 72,79%
80° 43.44% 56.67 %
89° 89.97 % 10.03 %

Fig 184 The amount of reflected light is dependent on the angle of incidence A graph demonstrates the dependence of the proportion of the reflected light to the angle of incidence; the intensity of the incidence at right angle does not sink to zero, but retains a residual quality R0 (Fig, 184).

R0 is termed luster intensity and is dependent solely in the refractive index(= n) as explained in the following paragraph:

R0 ={(n-1) / (n+1)}2

For diamond n = 2.42. Thus the equation reads:

R0 ={(1.42) / (3.42)}2 = 0.1723 = 17.23%

The greater is R0 the greater the external brilliance; the greater n, the greater R0.The color of light does not alter when reflected by a diamond. The reflected ray, the luster ray, is of the same color as the incident light. This is most important in the determination of the color of a diamond. For example, in-a room with yellow walls the incident light will be yellow, and consequently also the reflected light. This can lead to incorrect grading of the color.

Brilliance Internal brilliance